火山研究情報 トップへ

伊豆大島火山自然電位モニタリング

数値シミュレーション

自然電位の発生メカニズム

　自然電位の発生メカニズムについてやや詳しく説明します。自然電位はなかば定常的に地表に現れる電位分布ですが、ここではその成因として流動電位を考えます。大地の空隙の固液界面に電気二重相が形成されることによってゼータ電位と呼ばれる電位勾配が生じた状態で、液相が流動することによって発生する電位を流動電位と呼びます。多くの場合，ゼータ電位は負のため、流れとともに正の電荷が運ばれます。一方、流動電位を解消するように大地に拡散電位が生じ、それを地表で観測したものが自然電位となります。通常、熱水の上昇域の地表では正電位異常が発生します。そのため、多くの火山地域や地熱地域において自然電位の正異常が観測され、熱水の上昇域であると解釈されています（Zlotnicki and Nishida, 2003）。ただしゼータ電位はpHに依存し、酸性環境下では小さくなることが知られています（Ishido and Mizutani, 1981）。熱水の上昇域でも、酸性熱水であれば自然電位の正異常は発生しづらくなります。
　一方、降雨によっても自然電位は発生しますので、一般的に地表から深度が増すにつれて電位は高くなります。そのため、標高が増すにつれて地形効果によって自然電位は低くなります。山頂部に熱水上昇に伴う正異常がある火山の場合、地形効果によって麓から山頂に向かっていったん電位が低下するので、W字型の自然電位分布を示すことが知られています（Ishido, 2004）。
　流体の流動によって発生する自然電位は媒質の比抵抗が不均質であることによっても変化します。そのため降雨の浸透のみによっても、地形効果だけでは説明できない異常が生じます（Onizawa et al., 2009）。熱水循環が活発なところでは変質帯が発達しますが、変質帯は顕著な低比抵抗を示すことがあります。従って、自然電位分布から熱水循環を定量的に解析するためには、媒質の比抵抗構造を評価することが重要になります。図13はその様子を模式的に示したものです。左上は雨水が均質な比抵抗の大地に浸透した時の大地の電位分布を示し、右上は大地の比抵抗が不均質な場合の電位分布を示します。右上の状況に、火山活動による電位分布（左下）を加えたものが実際に観測される電位分布（右下）となります。したがって、火山活動による電位分布（左下）を得るためには、実際に観測される電位分布（右下）から不均質な大地を雨水が浸透する際の電位分布（右上）を評価することが必要となります。雨水や比抵抗構造の影響を取り除き、火山活動の活発化によって火山性流体の流動が生じた場合にどのような自然電位の変化が現れるかを数値シミュレーションから調べ、自然電位の定点観測から火山活動の推移を予測するための資料とします。

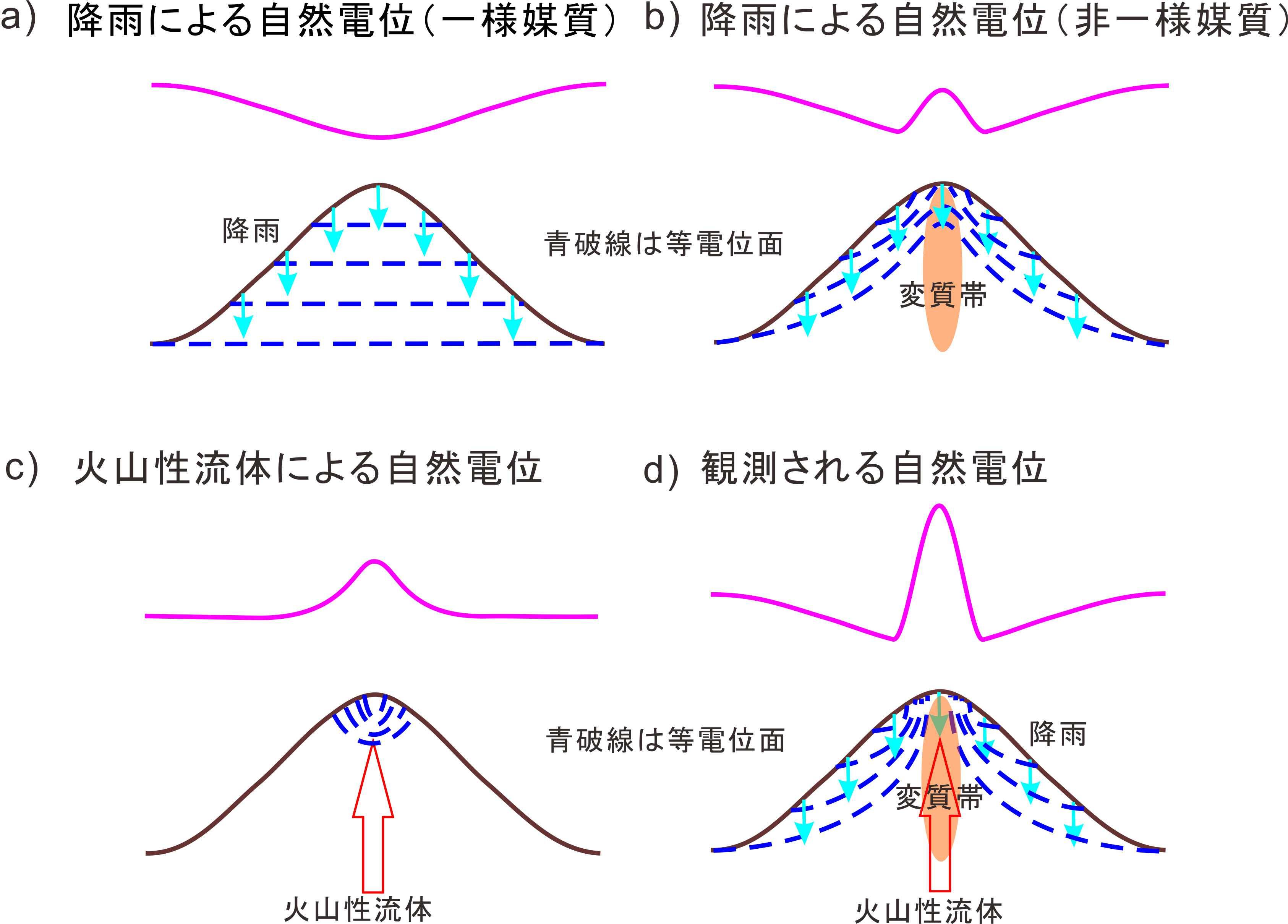
図13　自然電位の発生様式の模式図
各図で青破線は山体内に生じる電位をピンク線は地表面に沿って生じる電位（自然電位）を示す。

　　

解析手法

　解析手順は図14のようになります。まず、雨水浸透による地下水流動をシミュレーションし、その結果から自然電位分布を計算します。地下水流動のシミュレーションでは透水係数や空隙率などの水理パラメータを必要としますが、これらのパラメータを変えた計算を行い、自然電位の観測値と矛盾しない結果を得ます。次に雨水浸透の流動シミュレーションの結果を初期条件として、火山活動の活発化に伴い想定される、熱水や水蒸気の地下深部からの上昇を含む地下水流動をシミュレーションします。そして、その結果から自然電位分布の経時変化を計算し、自然電位連続観測点で変動を予測することにします。なお、自然電位を計算する際には大地の比抵抗を必要としますが、既に得られている3次元比抵抗構造（比抵抗構造の項参照）を用います。

図14　解析手順

　地下水流動のシミュレーションは、大地の空隙を、液相（地下水、熱水）ないしは気相（空気、水蒸気、火山ガス）またはその混相が流動するときの状態と熱伝達を計算します。計算のターゲットとなる大地を多孔質媒質とみなしてグリッドに分割し、それぞれの要素内で、ダルシー流を仮定した質量保存則とエネルギー保存則を解くことによって、圧力、温度、気液比などを求めます。その際に計算領域の境界条件や初期条件、雨水や地下深部からの熱水を想定したソースを設定します。また、大地の水理的な特性である透水係数や空隙率などのパラメータを与えます（図15）。

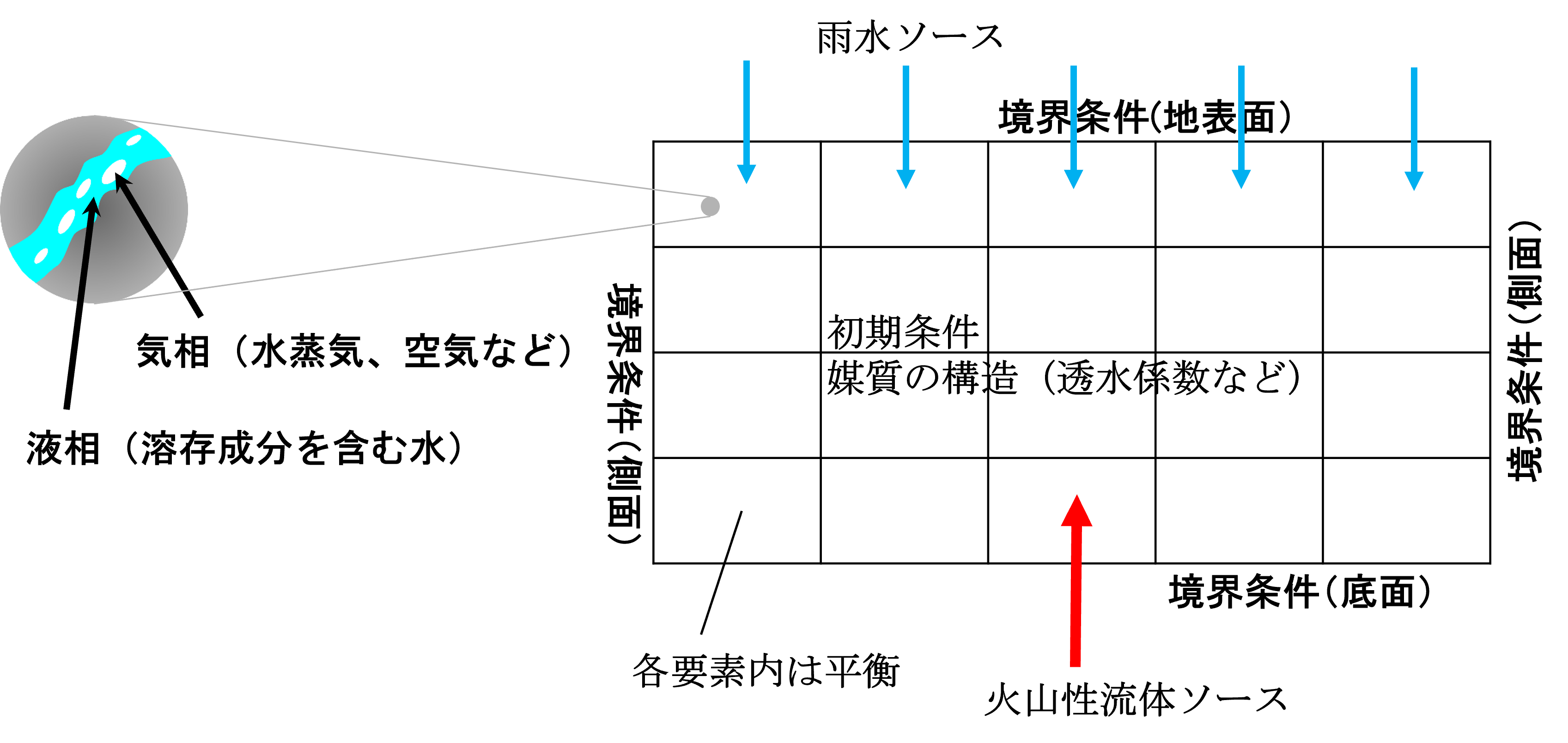
図15　地下水流動シミュレーションの概要

　シミュレーションでは、比抵抗の3次元インバージョン解析（比抵抗構造の項参照）で用いたグリッドの一部を用います。こうすることによってシミュレーション結果から自然電位分布を計算する際に比抵抗値を与えやすくなります。3次元インバージョン解析で用いたグリッドの中央部の約10 km四方を切り抜き，産総研で所有する熱水流動のシミュレータ「STAR」(Pritchett,1995)を用いて計算を行いました。流体は水，空気，塩化ナトリウムの3成分系とし、雨水には一般的な塩分濃度（10^-3 mol/l）を与えています。地表面は温度・圧力一定、その他は断熱・不透水境界としました。ただし、側面に接するグリッドに圧力一定となる流体のソース、底面に接するグリッドに温度一定となる熱量のソースを与えています。地殻熱流量に即した温度分布および静水圧を初期状態としましたが、伊豆大島では地下水面が海水準付近に位置することから、海水準より上部では液相飽和度0.2の空気及び水の2成分2相状態としました。
　大地の水利的特性を表すパラメータについては、何回か計算を行い、後で示すような計算される自然電位分布が観測結果に近いものを採用しています。透水係数は、海水準下2kmより浅部については、Onizawa et al., 2009 に従い、地下水面がほぼ海水準になるという条件から水平方向、鉛直方向ともに1.0×10^-13m²としています。カルデラ内北部で自然電位が高い値を示す領域は、緻密な溶岩からなると想定し迂回係数（tortuosity）を1.3としました(他の部分は1.6)。また櫛形山および三原山頂の噴気地帯に相当するところおよびその直下では透水係数を1.0×10^-11 m²としました。一方、海水準下2kmより深部では、Ingebritsen and Manning and Ingebritsen(1999)を参考にして深くなるにつれて水平、鉛直方向ともに1.00×10^-15 m²から1.00×10^-17 m²に変化させています。 熱水系の流動様式は媒質の透水係数に大きく依存します。今回の計算結果はあくまでもここで想定したような透水係数に基づいたものであることに注意が必要です。

解析結果

雨水の浸透のみ

　雨水浸透による地下水流動のシミュレーションでは、地表に本地域の年平均降水量（3200 mm）を与え、降雨の50 %が浸透すると仮定しています。定常状態とみなせるような、1000年間にわたって雨水を地表から浸透させています。その時の雨水浸透の様子を図16に示します。

図16　計算領域内の雨水浸透の様子（紫矢印）
白枠はグリッドを示す。左図は南側から真上、斜め上、真横から眺めたもの。右図は斜め下から眺めたものを拡大した。地形は基盤地図情報数値標高モデル(国土地理院)を利用して作成

　この地下水流動のシミュレーションの結果から得られる体積流量分布に基づいて，STARのポストプロセッサを用いて自然電位分布を計算しました。その際にゼータ電位は約-30 mVとしています。また、各グリッドへ3次元インバージョン解析から得られている比抵抗値を与えています（比抵抗構造の項参照）。自然電位の計算はMatsushima et al., 2017の方法にならったていますが、各グリッドに比抵抗を与えているところが従来の方法とは異なっています。計算された自然電位分布（図17右側）は、観測されたもの（図17左側）を比較的よく再現していることがわかります。そこで、この結果を初期状態として、熱水や火山ガス（火山性流体）が深部より上昇してきたときの地下水流動のシミュレーションを次に行います。

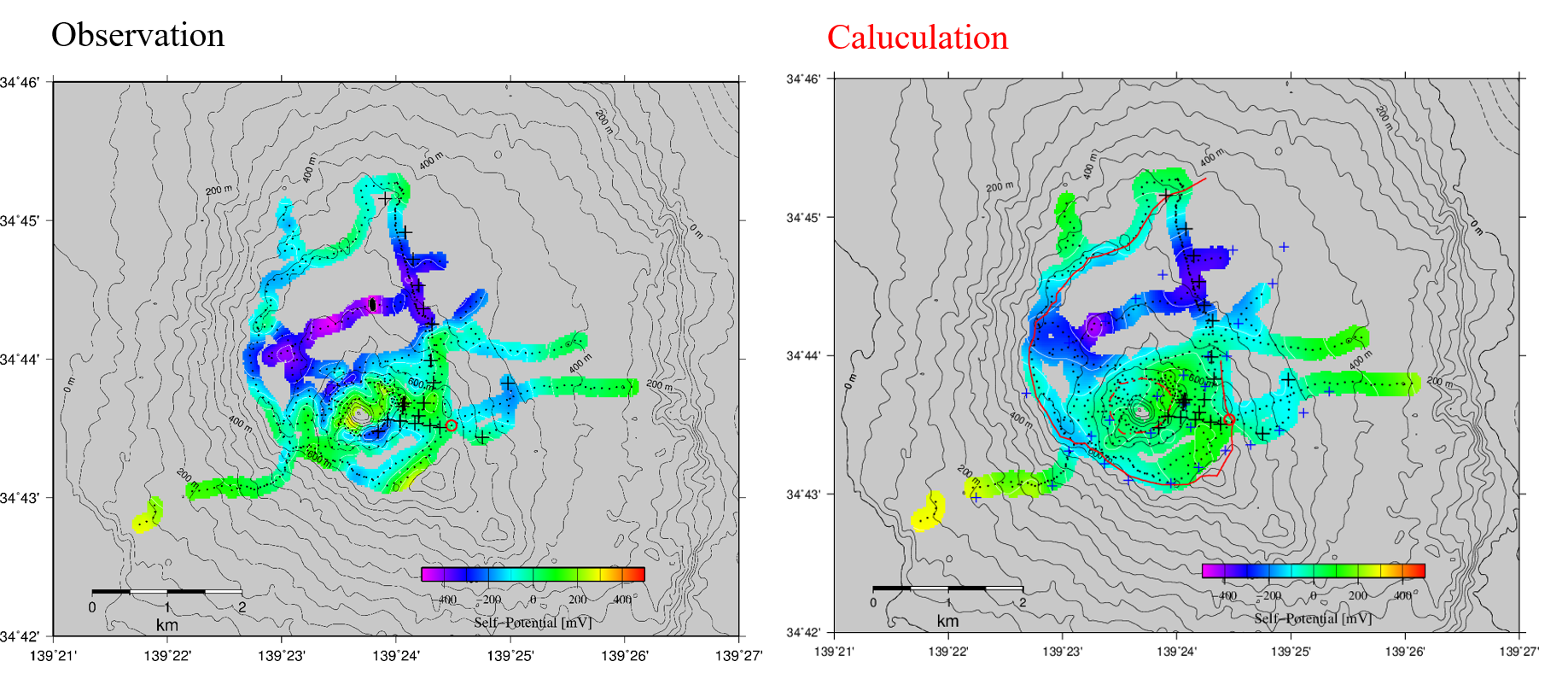
図17　自然電位分布
左図：観測結果、右図：雨水の流動による計算結果

深部からの火山性流体の上昇

　地表からの雨水浸透は前回と同様にしたまま、地下深部に流体のソースを置いて、ソースの流量と比エンタルピーを様々に変えた計算を行い、火山性流体の深部からの上昇をシミュレーションします。それに伴う自然電位分布を計算し、どのような自然電位変動が現れるか調べ、観測される自然電位変動から地下の状態を予測するための資料とします。ソースの位置は三原山の山頂部でみられる噴気地帯の直下で海水準下約2kmの深度としました。ソースの流量としては、伊豆大島の1986年噴火後の1988-90年に観測された噴煙による地表からの水蒸気放出量160kg/s（Kazahaya et al., 1994）を該当するグリッドの体積(水平方向400 m、厚さ300 m）で除した値3.4×10^-6 kg/sm³を参考とし、5.0×10^-6 kg/sm³にしました。また比エンタルピについては当該深度の圧力（18MPa）と温度320 ℃の時の値2.8×10⁶ J/kgを参考にして与えています。得られた結果から、三原山を中心とした東西および南北の鉛直断面を図18に示します。色は温度、矢印は流体の流動方向とその相対的な大きさを示します。なおこの計算では、透水係数として、海抜下2kmより上部では10^-13 m²ですが、地表で噴気兆候が見られる場所の直下と、比抵抗が10 Ω・m以下を示すグリッドの透水係数は10^-11 m²としています。その結果、温度分布と比抵抗構造（図10および12）が良い一致を示しており、熱水が対流することにより低比抵抗域が現れているとした解釈を裏付ける結果となっています。このような海水準下での熱水対流が伊豆大島火山の特徴ではないかと考えています。

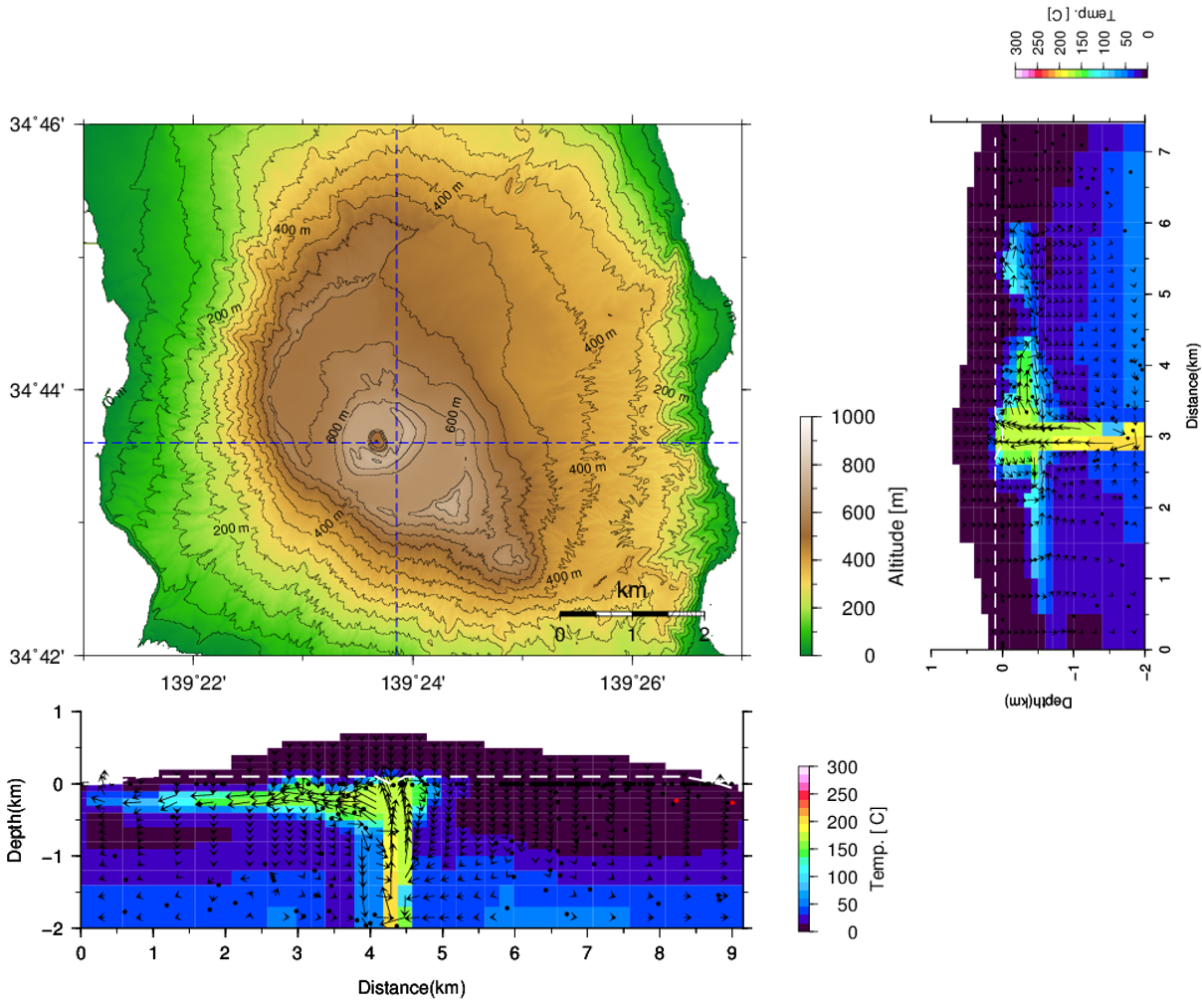
図18　熱水流動の数値シミュレーション結果、東西および南北鉛直断面

　しかしながらこの状態では、深部からの火山性流体が海水準を超えて浅部へ上昇することができず、地表に現れる自然電位には顕著な影響を及ぼしません。このことは顕著な経年変化の見られない現状と矛盾していません。仮に深部からの火山性流体の上昇量が増加し、海水準を突き抜けて地表へ到達した場合にどのような自然電位の変化が現れるかを計算してみました。ここでは、深部のソースの流量を一桁大きく5.0×10^-5 kg/sm³としています。ただし、海水準より浅部の不飽和層を表現するために、これまでは空気と水の2成分を考慮していましたが、それだとこの計算では不安定になってしまうため、水の1成分とし、その場所の温度に対応する飽和蒸気圧を与えることによって疑似的に不飽和層を表現しています。得られた結果から、三原山を中心とした東西および南北の鉛直断面を図19に示します。深部から上昇してきた火山性流体は海水準を突破して浅部へ上昇し、海水準より浅部では液相の水と水蒸気の2相状態となっています。図では全体的な流動方向しか示していないため明示されていませんが、この部分では液相の水の下降する一方、水蒸気は上昇するカウンターフローとなっています。

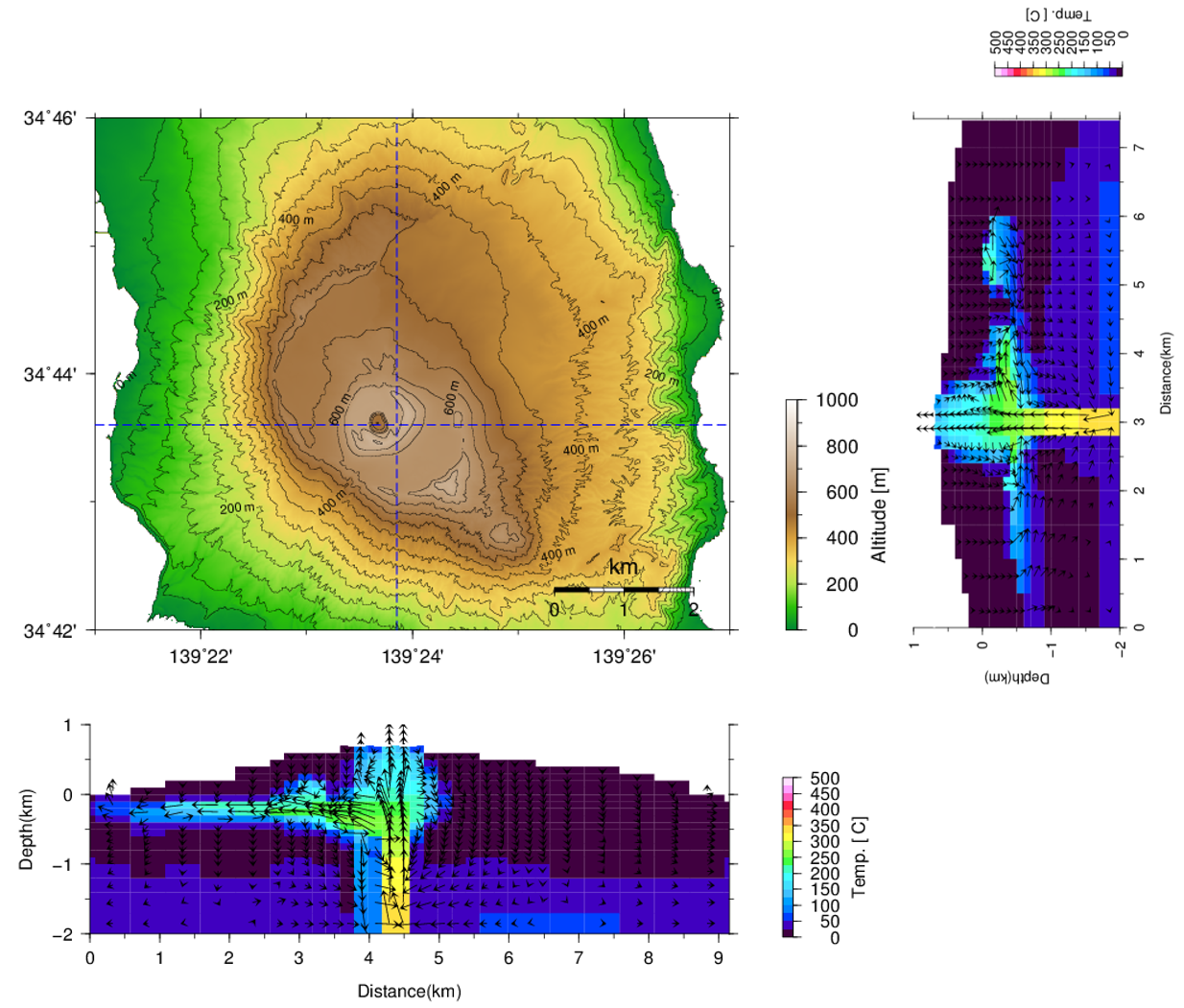
図19　熱水流動の数値シミュレーション結果その2、東西および南北鉛直断面

　このときの地表での自然電位分布を図20に示します。現状を表す計算結果（図17）と比べ、三原山山頂部の自然電位が顕著に減少していることが分かります。これは、下降する液相の水は電荷を運び自然電位分布に影響するのに対して、上昇する水蒸気は電荷を運ばないため自然電位に影響しないことによります。従って、今後火山活動が活発化し、深部からの脱ガスに伴う火山性流体の上昇量の増加に伴って、特に三原山山頂域の自然電位が低下することが予想されます。一般に、地熱地帯等では熱水の上昇域に自然電位の正異常が現れることが知られていますが、伊豆大島火山の場合にはこれとは逆の傾向を示すことが予想され注意が必要です。

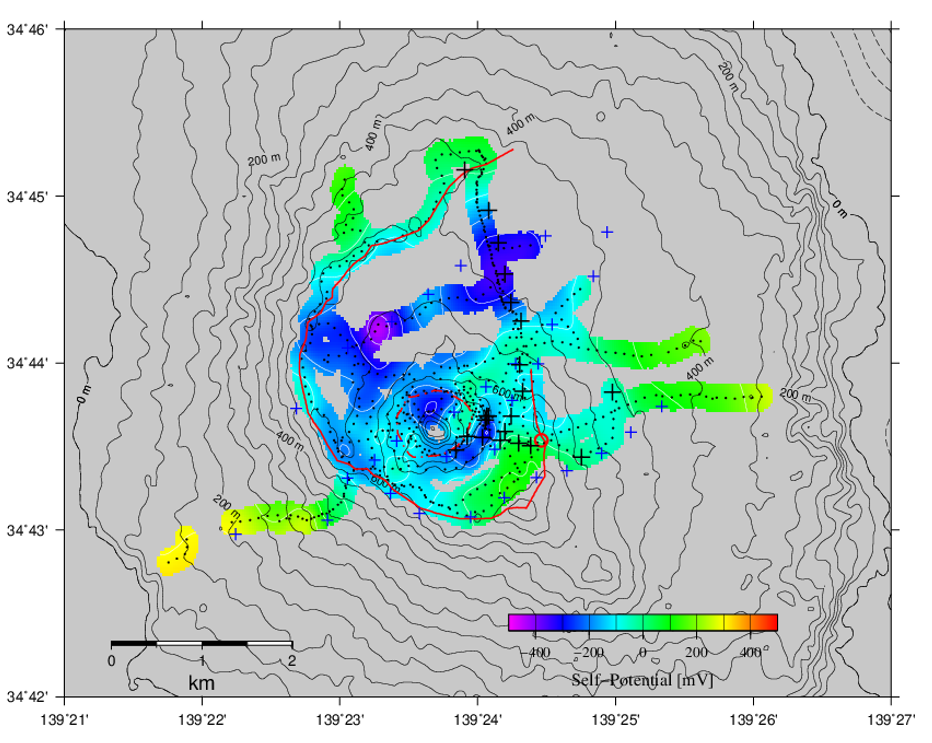
図20　熱水流動の数値シミュレーション結果その2から得られる自然電位分布

参考文献

Ishido T. (2004) Electrokinetic mechanism for the “W”-shaped self-potential profile on volcanoes. Geophys. Res. Lett. 31
Ishido T. and Mizutani H. (1981) Experimental and theoretical basis of electrokinetic phenomena in rock‐water systems and its applications to geophysics. J.Geophy.Res 86: 1763-1775.
Kazahaya K., Shinohara H. and Saito G. (1994) Excessive degassing of Izu-Oshima volcano: magma convection in a conduit. Bull. Volcanology. 56, 207-215.
Manning C. E. and Ingebritsen S. E. (1999) Permeability of the continental crust: Implications of geothermal data and metamorphic systems. Reviews of Geophysics. 37, 127-150.
Pritchett JW (1995) STAR: a geothermal reservoir simulation system.Proceedings of world geothermal congress 1995, pp. 2959–2963,Int. geothermal Assoc., Florence.
Zlotnicki, J. and Nishida, Y. (2003) Review on morphological insights of self-potential anomalies on volcanoes24, Surv. Geophys. 24: 291-338.